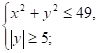27. Решение системлинейных неравенств.
Пусть заданынесколько неравенств с одним неизвестным. Если требуется найти число, котороеявляется решением всех данных неравенств, то совокупность этих неравенствназывают системой неравенств.
Решением системы неравенств с однимнеизвестным называется то значение неизвестного, при котором каждое неравенствосистемы обращается в верное числовое неравенство. Множество решений системынеравенств есть пересечение множеств решений входящих в нее неравенств.
Решить систему неравенств – это значит найтивсе решения этой системы или установить, что их нет.
Неравенства, входящие в систему, объединяются фигурной скобкой. Иногдасистемы неравенств записывают в виде двойного неравенства. Например, систему ![]() можно записать так: 2 < 3x-1 < 8.
можно записать так: 2 < 3x-1 < 8.
Решение системы линейных неравенств с одной переменной сводится кследующим случаям. Будем считать, что a < b:
![]() ( 1 )
( 1 ) ![]() ( 2)
( 2) ![]() ( 3 )
( 3 ) ![]() ( 4 )
( 4 )
В случае ( 1 ) решением системы служит промежуток (b
в случае ( 2 ) – промежуток ( ab) (рис 1, б);
в случае ( 3 ) – промежуток ( -∞; a) (рис 1, в);
в случае ( 4 ) система не имеет решений (рис 1, г).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
a b x a b x a b x a b х
а) б) в) г)
Рис.1.
Две системы неравенств называют равносильными, если они имеют общеемножество решений, удовлетворяющих этим неравенствам. Равносильность системнеравенств обозначается также, как и равносильность систем уравнений, т.е. спомощью знака ![]() .
.
Пример 1. Решить систему неравенств ![]()
Решение. Имеем ![]()
![]()
На координатной прямой изобразиммножество чисел, удовлетворяющих последней системе неравенств ( рис.2). Изрисунка видно, что эта система, а значит, и данная система не имеют решений.
-2,2 3 х Рис.2.
Ответ: система не имеет решений.
Пример 2. Решить систему неравенств 
Решение. Заменим каждое неравенство системыравносильным ему неравенством, получим систему


Изобразим на координатной прямой множество чисел, удовлетворяющихпоследней системе неравенств ( рис. 3).
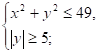 |
2 3,6 8 х Рис. 3.
Множество решений есть промежуток [3,6; 8).
Ответ: [3,6; 8).
Пример 3. Решить систему неравенств 
Решение. Решим первое неравенство: 3х – 4 < 8x + 6, -5x < 10, x > -2. Оно выполняется при x > -2.
Решимвторое неравенство : 2x — 1> 5x -4, -3x > -3, x < 1. Оновыполняется при x < 1.
Решимтретье неравенство : 11x – 9 ≤ 15x +3< -4x ≤ 12, x ≥ -3. Оновыполняется при х ≥ -3.
Все три данных неравенства верны при х ![]() ( -2;1).
( -2;1).
 |
![]()
-3 -2 1 х Рис. 4.
Ответ: (-2; 1).
Пример 4. Решить систему неравенств 
Решение.

![]()

![]()

Ответ: х >3.
Пример 5. Решить систему неравенств 
Решение.



Ответ: ![]()
Пример 6. Решить систему неравенств 
Решение. 
![]()
![]()
![]()
![]()

Данное неравенство верно при x < 0.
Ответ: ( — ∞; 0).
Пример 7. Решить системунеравенств 
Решение. 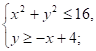
![]()

![]()
![]()
Данное неравенство верно при x > -3.
Ответ: ( -3; +∞).
Пример 8. Укажите наибольшее инаименьшее целое число, удовлетворяющее системе неравенств
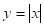
Решение.
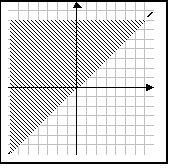

![]()
![]()
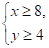
Ответ: -31; 2.
Пример 9. Длина основания равнобедренного треугольника равна 12 см.Каким числом может быть выражена длина боковой стороны, если известно, чтопериметр треугольника меньше 80 см ?
Решение. Пусть длина боковой стороны равна хсм.
Тогда ![]()
![]()
![]()
Длина боковой стороны может быть выражена любым числом из промежутка(6; 34).
Ответ: любым числом их числового промежутка ( 6; 34).
Пример 10. Подберите значения параметров a и b так, чтобы множество решений системы неравенств
![]()
а) было пусто;
б) состояло из одного элемента;
в) представляло собой промежуток
г) представляло собой промежуток [5;+∞).
Решение.Первое неравенство системы запишем в виде: 2х ≥ 10, х ≥5. Второе неравенствосистемы запишем в виде ах ≤ b+1.
а) Множество решений системы будетпусто, если
a>0, x1 ≤(b+1):a x1 5 x
Рис.5.
Т.е. х1 < 5. Выберемтакие а и b, чтобы ![]() .Например, а = 2, b = 7.
.Например, а = 2, b = 7.
б) Множество решений системынеравенств будет состоять из одного элемента, если
a>0, x1 =(b+1):a x 1 = 5 x
Рис.6.
Т.е. х1 = 5. Выберем такиеа и b, чтобы ![]() . Например, а = 3, b = 14.
. Например, а = 3, b = 14.
в) множество решений данной системынеравенств будет представлять собой промежуток
a>0, x1 ≤(b+1):a 5 10 x
Рис.7.
Т.е. х1 = 10. Выберемтакие а и b, чтобы ![]() .Например, а = 1, b = 9.
.Например, а = 1, b = 9.
г) множество решений данной системынеравенств будет представлять собой промежуток [5; +∞), если
a < 0, x1 ≥ (b+1):a х1=5 x
Рис.8.
Т.е. х1 = 5. Выберем такиеа и b, чтобы ![]() . Например, а = -2, b = -11.
. Например, а = -2, b = -11.
Ответ: а) например, а = 2, b = 7; б) например, а= 3, b = 14;
в) например, а = 1, b = 9;
г) например, а = -2, b = -11.
Пример11. Изобразить множество точек на плоскости,определяемое системой неравенств ![]()
Решение. Так какх + у < 1, то у < 1 – х; так как 2х – у < 2, то у > 2х – 2.Множество, задаваемое системой неравенств состоит из точек, лежащих под прямойу = 1 – х и одновременно над прямой у = 2х – 2. Т.е. множество решений каждогоиз этих линейных неравенств есть полуплоскость. Множество, определяемоесистемой этих неравенств есть пересечение полуплоскостей.
![]() у
у

![]()

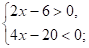 у=1-х
у=1-х
у=2х-2
1
0 1 х
-2
Рис. 9.
Пример 12. На координатной плоскости покажите с помощью штриховки множество точекF, задаваемое системой неравенств ![]() Какуюфигуру представляет собой множество F?
Какуюфигуру представляет собой множество F?
![]() Решение. Множество, задаваемое системой неравенств состоит из точек, лежащихпод прямой у = 5х + 4 и одновременно над прямой у = 5х +1. Т.е. множестворешений каждого из этих линейных неравенств есть полуплоскость. Множество,определяемое системой этих неравенств есть полоса.
Решение. Множество, задаваемое системой неравенств состоит из точек, лежащихпод прямой у = 5х + 4 и одновременно над прямой у = 5х +1. Т.е. множестворешений каждого из этих линейных неравенств есть полуплоскость. Множество,определяемое системой этих неравенств есть полоса.
y F
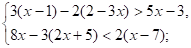 |
у = 5х + 4
у = 5х + 1
![]() 0 х
0 х
Рис. 10.
Ответ:полоса.
Пример 13. На координатной плоскости покажите с помощью штриховки множество точекF, задаваемое системой неравенств ![]() Какуюфигуру представляет собой множество F?
Какуюфигуру представляет собой множество F?

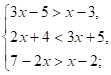
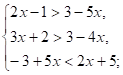 Решение. Множество, задаваемое системой неравенств состоит из точек, лежащихпод прямой у = -2х +4 и одновременно над прямой у = 3х +1. Т.е.множество решений каждого из этих линейных неравенств есть полуплоскость.Множество, определяемое системой этих неравенств есть угол.
Решение. Множество, задаваемое системой неравенств состоит из точек, лежащихпод прямой у = -2х +4 и одновременно над прямой у = 3х +1. Т.е.множество решений каждого из этих линейных неравенств есть полуплоскость.Множество, определяемое системой этих неравенств есть угол.
![]() у = -2х + 4
у = -2х + 4
4
F
1
![]() 0 2 х
0 2 х
у= 3х + 1
Рис.11. Ответ: угол.
Пример 14. На координатной плоскости покажите с помощью штриховки множество точекF, задаваемое системой неравенств  Какуюфигуру представляет собой множество F?
Какуюфигуру представляет собой множество F?
Решение.Множество, задаваемое системой неравенств состоит из точек, лежащих под прямой у = -2х +4 и одновременно под прямой у = х +2 и над прямой у = -5. Т.е.множество решений каждого из этих линейных неравенств есть полуплоскость.Множество, определяемое системой этих неравенств есть треугольник.
 у
у
 |


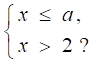 у = х + 2
у = х + 2
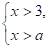 |
![]()
![]() 0 х
0 х
![]() у = -2х + 4
у = -2х + 4
![]()
![]() -5
-5
![]()
![]() у = -5
у = -5
Рис.12.
Ответ:треугольник.
Пример 15. На координатной плоскости покажите с помощью штриховки множество точек F, задаваемое системой неравенств 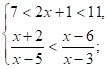 Какуюфигуру представляет собой множество F?
Какуюфигуру представляет собой множество F?
Решение. Множество, задаваемое системой неравенств состоит из точек, лежащихпод прямой у = -х + 6 и одновременно под прямой у = 2х +8 и над прямой у= -х + 2 и над прямой 2х + 2. Т.е. множество решений каждого из этих линейныхнеравенств есть полуплоскость. Множество, определяемое системой этих неравенствесть параллелограмм.

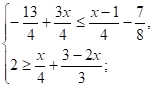
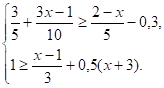 у
у
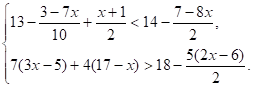 |
![]() у = 2х + 2
у = 2х + 2
![]() 6
6
 |
у = — х + 6
![]() у = 2х + 8
у = 2х + 8
2
![]() у = — х + 2
у = — х + 2
![]() -4 –1 0 2 х
-4 –1 0 2 х
Рис.13.
Ответ:параллелограмм.
Пример 16. Задайте системой неравенств фигуру,показанную на рисунке 14 штриховкой.
|
|
|
Представленная информация была полезной? ДА 60.87% НЕТ 39.13% Проголосовало: 1536 |
а) б)
|
|
|
|
в) г)
Рис.14.
Решение. а) ![]()
б) Составимуравнение прямой, проходящей через точки ( 5; 0) и ( 0; 8): ![]()
![]() у = -1,6х + 8 – уравнение прямой,проходящей через точки ( 5; 0) и ( 0; 8).
у = -1,6х + 8 – уравнение прямой,проходящей через точки ( 5; 0) и ( 0; 8).
Искомая системанеравенств: 
в) ![]()
![]()
у = -х + 3 –уравнение прямой, проходящей через точки ( 3; 0) и ( 0; 3).


у = 0,5х + 3 –уравнение прямой, проходящей через точки ( -6; 0) и ( 0; 3).


у = 2х — 6 –уравнение прямой, проходящей через точки ( 3; 0) и ( 0; -6).
Искомая системанеравенств: 
г) Зная для каждойиз прямых, ограничивающих четырехугольник, координаты двух точек, записываем ееуравнение.
Искомая системанеравенств: 
Ответ: а) ![]() б)
б)  в)
в) г)
г) 
Пример 17. Задайте системой неравенств четырехугольник АВСD,вершинами которого служат точки: А ( -5; 0), В (1; 3), С ( 3; -1); D ( -2; -4).
Решение.
|
|
Четырехугольник АВСD ограничен прямыми АВ, ВС, CD, DA ( рис. 15). Зная координаты двух точек прямой, можно записатьуравнение этой прямой.
Для прямой АВимеем:
![]()
![]()
у = 0,5х + 2,5 – уравнение прямой АВ.
Рис. 15.
Для прямой ВСимеем: 

у = -2х + 5 –уравнение прямой ВС.
Для прямой СD имеем: 

у = 0,6х – 2,8 –уравнение прямой CD.
Для прямой DA имеем: 

у = ![]() x
x ![]() – уравнение прямой DA.
– уравнение прямой DA.
Искомая системанеравенств: 
Ответ: 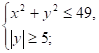
Пример 18. Покажите штриховкой множество точек плоскости, координаты которых удовлетворяютнеравенству: а) у > x![]()
![]()
![]() .
.
Решение. а) См. рис. 16, а.
б) Искомоемножество – множество точек, расположенных выше графика функции ![]() ( рис. 16, б).
( рис. 16, б).
в) Рассмотримотдельно каждую из координатных четвертей. В I четвертинеравенство примет вид у > х. Ему соответствует множество точек первогокоординатного угла, расположенного выше биссектрисы этого угла. Во II и III четвертях, неравенству удовлетворют координатылюбой из точек. В IV четверти неравенство примет вид –у> x, т.е. у < -х. Ему соответствует множество точекчетвертого координатного угла, расположенного ниже его биссектрисы ( рис. 16,в).
г) Рассматриваемотдельно каждую из координатных четвертей ( рис. 16, г).
|
|
|
|
а) б)
|
|
|
|
в) г)
Рис.16.
Пример 19. Покажите штриховкой множество точек координатнойплоскости, координаты которой удовлетворяют неравенству:
а) (х –8)(у – 4) ≥ 0; б) ( х – 2)(у + 6) ≤ 0; в) х2 – у2 ≥0; г) х2 – 4у2 ≤ 0.
Решение. а)Неравенство верно, если ![]() или
или ![]() ( рис. 17, а).
( рис. 17, а).
б) Неравенство верно, если ![]() или
или ![]() (рис. 17, б).
(рис. 17, б).
в) Представим неравенство в виде ( х – у)( х +у0 ≥ 0. Неравенство верно, если ![]() или
или ![]() ( рис. 17, в).
( рис. 17, в).
г) Представим неравенство в виде ( х – 2у)(х +2у) ≤ 0. Неравенство верно, если ![]() или
или ![]() ( рис. 17, г).
( рис. 17, г).
|
|
|
|
а) б)
|
|
|
|
в) г)
Рис.17.
Задания для самостоятельного решения
Решите систему неравенств:
1. 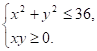
2. 
3. 
4. 
5. Укажитенаибольшее и наименьшее целое число, удовлетворяющее системе неравенств:

6. Подберите значение параметра a так, чтобы для системы неравенств ![]()
а)наименьшее целое число, удовлетворяющее системе, было равно 3;
б)наибольшее целое число, удовлетворяющее системе, было равно 12;
в) не существовало бы ни одного целого числа, удовлетворяющего системе.
7. Решитесистему неравенств : а) ![]() б)
б)![]()
в) ![]() г)
г) ![]()
8. Решитесистему неравенств:
а) ![]() б)
б)![]()
в)  г)
г)
9. Решитесистему неравенств:
а)  б)
б)
в)  г)
г)
10. Решитесистему неравенств:
а)  б)
б)
в) 
г) 
11. Прикаких значениях а система неравенств имеет хотя бы одно решение:
а) ![]() б)
б)![]() в)
в) ![]() г)
г) ![]()
12. Прикаких значениях а система неравенств не имеет решений:
а) ![]() б)
б)![]() в)
в) ![]() г)
г) 
13. Существуютли такие значения а, при которых решением системы неравенств ![]() является промежуток: а) ( 5; + ∞); б)( 3; +∞); в) [3; +∞); г) ( 2; +∞) ?
является промежуток: а) ( 5; + ∞); б)( 3; +∞); в) [3; +∞); г) ( 2; +∞) ?
14. Существуютли такие значения а, при которых решением системы неравенств ![]() является промежуток: а) ( -∞ ; 7); б) ( -∞; 5); в) ( -∞; 5]; г) ( -∞; 2) ?
является промежуток: а) ( -∞ ; 7); б) ( -∞; 5); в) ( -∞; 5]; г) ( -∞; 2) ?
15. Прикаких значениях а система неравенств ![]() неимеет решений?
неимеет решений?
16. Прикаких значениях а система неравенств  имеет хотя бы однорешение?
имеет хотя бы однорешение?
17. Решитедвойное неравенство : а) –3 < 3 – 2x < 1; б) –2< 3x – 1 < -1;
в) 0 < 4 – 3x< 2; г) 0 < 1 – 2x < 1.
18. Решитесистему неравенств:
а) ![]() б)
б)![]() в)
в) ![]() г)
г) ![]()
19.Решите систему неравенств:
а)  б)
б)  в)
в)  г)
г)
20. Найдитесередину промежутка, являющегося множеством решений системы неравенств:
а)  б)
б)
21. Найдитенаименьшее целое х, удовлетворяющее системе неравенств:

22. Найдитенаибольшее целое х, удовлетворяющее системе неравенств:

23. Прикаких значениях k и b множествоточек плоскости, задаваемое системой неравенств ![]() а)представляет собой полосу; б) представляет собой угол; в) пустое множество?
а)представляет собой полосу; б) представляет собой угол; в) пустое множество?
24. Запишитесистему неравенств, задающую на координатной плоскости множество точек,показанное штриховкой на рисунке 20.
|
|
|
|
а) б)
|
|
|
|
в) г)
Рис. 20.
Ответы: 1. х ![]() [-0,5; 0,5). 2. х
[-0,5; 0,5). 2. х ![]() (-3; -1). 3. х
(-3; -1). 3. х ![]() (2,4; 18). 4. х ≤ 0. 5. 6. а) например, а =1; б) например, а=0,5; в) например, а =13,2.
(2,4; 18). 4. х ≤ 0. 5. 6. а) например, а =1; б) например, а=0,5; в) например, а =13,2.
9. а)1<x<3; б) 4/7 < x <8/3; в) 1/7 < x <16/7; г) x> 4. 10. а) 0,05<x<0,1.
11. а) a<3; б) а<5; в) а ≤ 7; г) а ≥2. 12. а) а ≥ 2; б) а ≥ 2; в) а > 5; г) а ≤ 2.
13. а) а = 5; б) а ≤ 3; в), г) не существует. 14. а) Несуществует; б) а = 5; в) а > 5; г) а = 2.
15. а ≤ 2. 16. а > 21/127. 17. а) 1<x<3; б) –1/3 <x<0. 18. а)–0,5<x<0,6; б) 0,25<x<1/3.
19. а) х=1,5; в) 3,6< x <5; г) 1 < x ≤ 2,5. 20. а) 0,925; б) –0,5. 21. 1. 22.5.
23. а) при k = 3, b < -1; б) k ≠ 3, b – любое; в) k = 3 , b > -1. ( см. рис. 25)
|
|
|
|

![]()
![]()


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() у
у
![]()
![]() 0 2 х
0 2 х
Рис. 25.
24. а)  б)
б)  в)
в)  г)
г)