X-PDF

X-PDF

Дистанционные курсы для педагогов

Поделиться статьей

 

Муниципальноеобщеобразовательное бюджетное учреждение средняя общеобразовательная школа №2с. Инзер муниципального района Белорецкий район Республики Башкортостан

 

 

 

 

Рассмотрено ипринято           Согласовано                                     Утверждено

на заседанииМО                     Заместитель директора по УВР     Директор МОБУ СОШ №2

Протокол№_____                   ________Юмагужина З.А.              с. Инзер

от «___»_____20____г.         «___» _____20____г.                        _________Идрисов Р.Н.

Руководитель МО                                                                         Приказ№____

 _______ШагисултановаА.М.                                                             от «____»_____20_____г.

 

 

 

 

 

 

 

 

 

Рабочаяпрограмма

попредмету «Математика (алгебра)»

для9  класса

на2017-2018 учебный год

 

Срокреализации – 1 год

 

 

 

 

 

 

 

 

 

                                                                                             Составила

                                                                                        учитель   Сунаргулова Г.Б.                                                       

                                                                                                       

 

 

 

 

 

 

 

 

 

 

2017год

 

 

 

 Рабочаяпрограмма  по  алгебре  в  9 классе составлена на основе  следующих документов:

   

  1. Положение о рабочей программе учителя по ФК ГОС.

 

  1. Основная образовательная программа основного общего образования МОБУ СОШ № 2 с. Инзер.

 

  1. Примерной   программы основного общего образования по математике   М.: Просвещение , 2010 ( Стандарты второго поколения) ,

.Предметная линияучебников Ю.Н.Макарычева и других. 7-9 классы: пособие для учителей общеобразоват.организаций   / Н.Г.Миндюк.  М.:Просвещение , 2014

 

  1. Учебный  план МОБУ СОШ №2 с. Инзер на 2017– 2018 учебный год,      утверждённый  приказом №  63   МОБУ СОШ №3 с. Инзер от  24.08.2017г.

 

  1. Приказ по МОБУ СОШ № 2 с. Инзер от  24.08.2017 №  65     «Об утверждении Федерального Перечня учебников, планируемых к использованию в образовательном процессе в 2017-2018учебном году»

Данная программаобеспечена следующим учебником: Алгебра. 9  класс:  учебник для общеобразовательныхучреждений с приложением на электронном носителе / Ю.Н.Макарычев, Н.Г.Миндюк,К.И.Нешков, С.Б.Суворова; под ред.С.А.Теляковского.- 19-е изд.- М.:Просвещение, 2014

Количество часов внеделю   3ч, в год- 98                                           

          

 

 

Общая характеристикаучебного предмета.

Математическое образование в основнойшколе складывается из сле­дую­щих содержательных компонентов (точные названияблоков): арифме­тика алгебра геометрияэлементы комбинаторики,теории вероятно­стей, статистики и логики. В своей совокупности ониотражают богатый опыт обучения математике в нашей стране, учитывают современныетенденции оте­чественной и зарубежной школы и позволяют реализоватьпоставленные пе­ред школьным образованием цели на информационно емком ипрактически значи­мом материале. Эти содержательные компоненты, развиваясь напротя­жении всех лет обучения, естественным образом переплетаются и взаимодейст­вуютв учебных курсах.

Алгебранацелена на формирование математического аппарата для реше­ния задач изматематики, смежных предметов, окружающей реальности. Язык алгебры подчеркиваетзначение математики как  языка для построения матема­тических моделей,процессов и явлений реального мира. Одной из основных задач изучения алгебрыявляется развитие алгоритмического мышления, необ­ходимого, в частности, дляосвоения курса информатики; овладение навыками дедуктивных рассуждений.Преобразование символических форм вносит свой специфический вклад в развитиевоображения, способностей к математиче­скому творчеству. Другой важной задачейизучения алгебры является получе­ние школьниками конкретных знаний о функцияхкак важнейшей математиче­ской модели для описания и исследования разнообразныхпроцессов (равно­мерных, равноускоренных, экспоненциальных, периодических идр.),для фор­мирования у учащихся представлений о роли математики в развитиицивилиза­ции и культуры.

Элементы логики,комбинаторики, статистики и теории вероятно­стейстановятся обязательным компонентом школьного образования, усили­вающим егоприкладное и практическое значение. Этот материал необходим, прежде всего, дляформирования функциональной грамотности – умений вос­принимать и анализироватьинформацию, представленную в различных фор­мах, понимать вероятностный характермногих реальных зависимостей, произ­водить простейшие вероятностные расчеты.Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрениеслучаев, перебор и подсчет числа вариантов, в том числе в простейших прикладныхзадачах.

При изучении статистики и теориивероятностей обогащаются представ­ления о современной картине мира и методахего исследования, формируется понимание роли статистики как источника социальнозначимой информации, и закладываются основы вероятностного мышления.

Цели обучения:

· овладениесистемой математических знаний и умений, необхо­димых для применения впрактической деятельности, изучения школьных естествен­нонаучных  дисциплин набазовом уровне, а также продолжения образования;

· формированиепредставлений об идеях и методах математики как универ­сального языка науки итехники, средства моделирования яв­лений и процессов, об идеях и методахматематики;

· интеллектуальноеразвитие, развитие логического мышления, пространственноговоображения, ясности и точности мысли, алгоритмической культуры, интуиции,способности к преодолению трудностей, критичности мышления на уровне,необходимом для дальнейшего обучения;

· воспитание средствами математикикультуры личности: отно­шения к ма­тематике как частиобщечеловеческой культуры: знакомство с историей раз­вития математики,эволюцией математических идей, пони­мания значимости математики дляобщественного прогресса

 

 

 

 

Место предмета в федеральном базисном учебном плане

Согласно Федеральному базисномуучебному плану на изучение матема­тики в 9 классе отводится не менее 170    часов из расчета 5  ч в неделю, при этом разделение часов на изучениеалгебры и геометрии может быть следующим:3 часа в неделю алгебры, итого 102 часа;2 часа в неделю геометрии, итого 68 ча­сов.

В соответствии сучебным планом МБОУ СОШ № 2  с. Инзер на изучение курса алгебры в 9 классеотводится 3 часа в неделю, всего   ча­сов в год

 

 

 

 

 

ТРЕБОВАНИЯ К УРОВНЮПОДГОТОВКИ УЧАЩИХСЯ

В результате изучения курса алгебры 9 классаобучающиеся должны:

знать/понимать

§ существо понятияматематического доказательства; при­меры доказа­тельств;

§ существо понятияалгоритма; примеры алгоритмов;

§ как используютсяматематические формулы, уравнения и не­равен­ства; примеры их применения длярешения математических и практических задач;

§ как математическиопределенные функции могут описы­вать реальные зависимости; приводить примерытакого описания;

§ как потребности практикипривели математическую науку к необходи­мости расширения понятия числа;

§ вероятностный характермногих закономерностей окружаю­щего мира; примеры статистическихзакономерностей и выво­дов;

§ каким образом геометриявозникла из практических задач землеме­рия;  примеры геометрических объектов иутверждений о них, важных для практики;

§ смысл идеализации,позволяющей решать задачи реальной действитель­ности математическими методами,примеры ошибок, воз­никаю­щих при идеализации.

уметь

§ составлять буквенныевыражения и формулы по условиям за­дач; осуще­ствлять в выражениях и формулахчисловые подста­новки и выполнять соответствующие вычисления, осуществлятьподстановку одного выражения в другое; выражать из формул одну переменную черезостальные;

§ выполнять основныедействия со степенями с целыми показа­телями, с многочленами и салгебраическими дробями; вы­полнять разложение много­членов на множители;выполнять тожде­ственные преобразования рациональ­ных выражений;

§ применять свойстваарифметических квадратных корней для вычисле­ния значений и преобразованийчисловых выражений, содержащих квадрат­ные корни;

§ решать линейные,квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двухлинейных уравнений и несложные нели­нейные системы;

§ решать линейные иквадратные неравенства с одной перемен­ной и их системы;

§ решать текстовые задачиалгебраическим методом, интерпре­тировать полученный результат, проводить отборрешений, исходя из формулировки задачи;

§ изображать числа точкамина координатной прямой;

§ определять координатыточки плоскости, строить точки с за­данными координатами; изображать множестворешений линей­ного неравенства;

§ распознаватьарифметические и геометрические прогрес­сии; решать за­дачи с применениемформулы общего члена и суммы нескольких первых членов;

§ находить значенияфункции, заданной формулой, таблицей, графиком по ее аргументу; находитьзначение аргумента по значе­нию функции, задан­ной графиком или таблицей;

§ определять свойствафункции по ее графику; применять гра­фические представления при решенииуравнений, систем, нера­венств;

§ описывать свойстваизученных функций (у = кх, где к0, у =кх + b,у=х2, у = х3, у =, у=, у = ах2 + bх+ с, у= ах2 + n,  у = а(х- m)2), строить их графики;

использовать приобретенные знания иумения в практиче­ской дея­тельности и повседневной жизни для:

§ выполнения расчетов поформулам, составления формул, вы­ражаю­щих зависимости между реальнымивеличинами; нахожде­ния нужной фор­мулы в справочных материалах;

§ моделированияпрактических ситуаций и исследовании по­строенных моделей с использованиемаппарата алгебры;

§ описания зависимостеймежду физическими величинами со­ответствую­щими формулами при исследованиинесложных прак­тических си­туаций;

§ интерпретации графиковреальных зависимостей между вели­чинами.

Элементы логики,комбинаторики, статистики и теории вероятностей

уметь

· проводитьнесложные доказательства, получать простейшие следст­вия из известных или ранееполученных утверждений, оценивать логическую правильность рассуждений,использовать примеры для ил­люстрации и контрпримеры для опроверженияутверждений;

· извлекатьинформацию, представленную в таблицах, на диаграм­мах, графиках; составлятьтаблицы, строить диаграммы и графики;

· решатькомбинаторные задачи путем систематического перебора воз­можных вариантов, атакже с использованием правила умножения;

· вычислятьсредние значения результатов измерений;

· находитьчастоту события, используя собственные наблюдения и гото­вые статистическиеданные;

· находитьвероятности случайных событий в простейших случаях;

использовать приобретенные знания иумения в практической дея­тельности и повседневной жизни для:

· выстраиванияаргументации при доказательстве (в форме моно­лога и диалога);

· распознаваниялогически некорректных рассуждений;

· записиматематических утверждений, доказательств;

· анализареальных числовых данных, представленных в виде диа­грамм, графиков, таблиц;

· решенияпрактических задач в повседневной и профессиональной дея­тельности сиспользованием действий с числами, процентов, длин, площадей, объемов, времени,скорости;

· решенияучебных и практических задач, требующих систематиче­ского перебора вариантов;

· сравненияшансов наступления случайных событий, оценки вероят­ности случайного события впрактических ситуациях, сопостав­ления модели с реальной ситуацией;

· пониманиястатистических утверждений.

 

           Cодержание  учебного предмета

 

Глава 1. Квадратичнаяфункция

Функция. Свойствафункций. Квадратный трехчлен. Разложение квадратного трехчлена на множители.Функция у = ах2 + bх + с, еёсвойства и график. Неравенства второй степени с одной переменной. Методинтервалов.

Цель: расширитьсведения о свойствах функций, ознакомить обучающихся со свойствами и графикомквадратичной функции, сформировать умение решать неравенства вида ах2+ bх + с>0 ах2 + bх+ с<0, где а0.

В начале темысистематизируются сведения о функциях. Повторяются основные понятия: функция,аргумент, область определения функции, график. Даются понятия о возрастании иубывании функции, промежутках знакопостоянства. Тем самым создается база дляусвоения свойств квадратичной и степенной функций, а также для дальнейшегоуглубления функциональных представлений при изучении курса алгебры и началанализа.

Подготовительным шагомк изучению свойств квадратичной функции является также рассмотрение вопроса оквадратном трехчлене и его корнях, выделении квадрата двучлена из квад­ратноготрехчлена, разложении квадратного трехчлена на множители.

Изучение квадратичнойфункции начинается с рассмотрения функции у=ах2, её свойств иособенностей графика, а также других частных видов квадратичной функции –функции у=ах2+n, у=а(х-m)2.Эти сведения используются при изучении свойств квадратичнойфункции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах2+ bх + с может быть получен из графика функции у =ах2 с помощью двух параллельных переносов. Приёмы построенияграфика функции у = ах2 + bх + сотрабатываются на конкретных примерах. При этом особое внимание следует уделитьформированию у обучающихся умения указывать координаты вершины параболы, ее осьсимметрии, направление ветвей параболы.

При изучении этой темыдальнейшее развитие получает умение находить по графику промежутки возрастанияи убывания функции, а также промежутки, в которых функция сохраняет знак.

Формирование уменийрешать неравенства вида ах2 + bх +с>0 ах2 + bх +с<0, где а0, осуществляется с опорой насведения о графике квадратичной функции (направление ветвей параболы еерасположение относительно оси Ох).

Обучающиеся знакомятсяс методом интервалов, с помощью которого решаются несложные рациональныенеравенства.

Обучающиеся знакомятсясо свойствами степенной функции у=хn причетном и нечетном натуральном показателе n.. Вводитсяпонятие корня n-й степени. Обучающиеся должны понимать смысл записей вида, . Ониполучают представление о нахождении значений корня с помощью калькулятора,причем выработка соответствующих умений не требуется.

Глава 2. Уравнения инеравенства с одной переменной

Целые уравнения.Уравнение с двумя переменными и его график. Системы уравнений второй степени.Решение задач с помощью систем уравнений второй степени.

Цель:систематизировать и обобщить сведения о решении целых с одной переменной,Выработать умение решать простейшие системы, содержащие уравнение второйстепени с двумя переменными, и текстовые задачи с помощью составления таких систем;выработать умение решать простейшие системы, содержащие уравнение второйстепени с двумя переменными, и текстовые задачи с помощью составления такихсистем.

В этой теме завершаетсяизучение рациональных уравнений с одной переменной. В связи с этим проводитсянекоторое обобщение и углубление сведений об уравнениях. Вводятся понятияцелого рационального уравнения и его степени. Обучающиеся знакомятся с решениемуравнений третьей степени и четвертой степени с помощью разложения на множителии введения вспомогательной переменной. Метод решения уравнений путем введениявспомогательных переменных будет широко использоваться дальнейшем при решениитригонометрических, логарифмических и других видов уравнений.

В данной темезавершаемся изучение систем уравнений с двумя переменными. Основное вниманиеуделяется системам, в которых одно из уравнений первой степени, а другоевторой. Известный обучающимся способ подстановки находит здесь дальнейшееприменение и позволяет сводить решение таких систем к решению квадратногоуравнения.

Ознакомлениеобучающихся с примерами систем уравнений с двумя переменными, в которых обауравнения второй степени, должно осуществляться с достаточной осторожностью иограни­чиваться простейшими примерами.

Привлечение известныхобучающимся графиков позволяет привести примеры графического решения системуравнений. С помощью графических представлений можно наглядно показатьобучающимся, что системы двух уравнений с двумя переменными второй степенимогут иметь одно, два, три, четыре решения или не иметь решений.

Разработанныйматематический аппарат позволяет существенно расширить класс содержательныхтекстовых задач, решаемых с помощью систем уравнений.

Глава 3. Уравнения инеравенства с двумя переменными

Уравнения с двумя переменнымии их системы. Неравенства с двумя переменными и их системы. Арифметическаяпрогрессия. Геометрическая прогрессия. Элементы комбинаторики. Начальныесведения о теории вероятностей

Цель: ознакомитьучащихся с геометрической интерпретацией на координатной плоскости множестврешений некоторых неравенств с двумя переменными и их систем.

Вводится понятиерешения неравенств с двумя переменными и системы таких неравенств,рассматривается вопрос об изображении соответствующего множества решений накоординатной плоскости.

Глава 4.Арифметическаяи геометрическая прогрессии

Арифметическая игеометрическая прогрессии. Формулы n-гочлена и суммы первых n членов прогрессии. Бесконечно убывающаягеометрическая прогрессия.

Цель: датьпонятия об арифметической и геометрической прогрессиях как числовыхпоследовательностях особого вида.

При изучении темывводится понятие последовательности, разъясняется смысл термина «n-йчлен последовательности», вырабатывается умение использовать индексное обозначение.Эти сведения носят вспомогательный характер и используются для изученияарифметической и геометрической прогрессий.

Работа с формулами n-гочлена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяетнеоднократно возвращаться к вычислениям, тождественным преобразованиям, решениюуравнений, неравенств, систем.

Рассматриваютсяхарактеристические свойства арифметической и геометрической прогрессий, чтопозволяет расширить круг предлагаемых задач.

 

Глава 5. Элементыкомбинаторики и теории вероятностей

Комбинаторное правилоумножения. Перестановки, размеще­ния, сочетания. Относительная частота ивероятность случайного события.

Цель: ознакомитьобучающихся с понятиями перестановки, размещения, сочетания исоответствующими формулами для подсчета их числа; ввести понятия относительнойчастоты и вероятности случайного события.

Изучение темыначинается с решения задач, в которых требуется составить те или иныекомбинации элементов и. подсчитать их число. Разъясняетсякомбинаторное правило умножения, которое исполнятся в дальнейшем при выводеформул для подсчёта числа перестановок, размещений и сочетаний. При изученииданного материала необходимо обратить внимание обучающихся на различие понятий«размещение» и «сочетание», сформировать у них умение определять, о каком видекомбинаций идет речь в задаче.

В данной темеобучающиеся знакомятся с начальными сведениями из теории вероятностей. Вводятсяпонятия «случайное событие», «относительная частота», «вероятность случайногособытия». Рассматриваются статистический и классический подходы к определениювероятности случайного события. Важно обратить внимание обучающихся на то, чтоклассическое определение вероятности можно применять только к таким моделямреальных событий, в которых все исходы являются равновозможными.

Глава 6. Повторение

Цель: Повторение,обобщение и систематизация знаний, умений и навыков за курс алгебры основнойобщеобразовательной школы

 

 

Критерии оценки

1.Оценка письменных контрольных работ обучающихся по математике.

 

Ответоценивается отметкой «5», если:

  • работа выполнена полностью;
  • в логических рассуждениях и обосновании решения нет пробелов и ошибок;
  • в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка«4» ставится в следующих случаях:

  • работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
  • допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка«3» ставится, если:

  •  допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка«2» ставится, если:

  • допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

 

2.Оценкаустных ответов обучающихся по математике

 

Ответоценивается отметкой «5», если ученик:

  • полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
  • изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
  • правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
  • показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
  • продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
  • отвечал самостоятельно, без наводящих вопросов учителя;
  • возможны одна – две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

 

Ответоценивается отметкой «4», если удовлетворяет в основном требованиям на оценку«5», но при этом имеет один из недостатков:

  • в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
  • допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
  • допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

 

Отметка«3» ставится в следующих случаях:

  • неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);
  • имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
  • ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
  • при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

 

Отметка«2» ставится в следующих случаях:

  • не раскрыто основное содержание учебного материала;
  • обнаружено незнание учеником большей или наиболее важной части учебного материала;
  • допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Грубымисчитаются ошибки:

  • незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
  • незнание наименований единиц измерения;
  • неумение выделить в ответе главное;
  • неумение применять знания, алгоритмы для решения задач;
  • неумение делать выводы и обобщения;
  • неумение читать и строить графики;
  • неумение пользоваться первоисточниками, учебником и справочниками;
  • потеря корня или сохранение постороннего корня;
  • отбрасывание без объяснений одного из них;
  • равнозначные им ошибки;
  • вычислительные ошибки, если они не являются опиской;
  • логические ошибки.

 

Кнегрубым ошибкам следует отнести:

  • неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного — двух из этих признаков второстепенными;
  • неточность графика;
  • нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
  • нерациональные методы работы со справочной и другой литературой;
  • неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

  • нерациональные приемы вычислений и преобразований;
  • небрежное выполнение записей, чертежей, схем, графиков.

 

 

 

 

 

 

 

Учебно-тематическоепланирование

 

№ п/п

Наименование разделов и тем

Кол.во часов

1

                  Повторение

2

2

Квадратичная функция.

22

3

Уравнения и неравенства с одной переменной

14

4

Уравнения и неравенства с двумя переменными

17

5

Арифметическая и геометрическая прогрессии

15

6

Элементы комбинаторики и теории вероятностей

13

7

Повторение

14

 

 

 

 

Литература

1.Примерная программа основного общего образования по математике   М.: Просвещение , 2010 (Стандарты второго поколения) ,

2.Предметная линияучебников Ю.Н.Макарычева и других. 7-9 классы: пособие для учителейобщеобразоват. организаций   / Н.Г.Миндюк.  М.:Просвещение , 2014

 

 3.Алгебра. 9  класс:  учебник для общеобразовательных учрежденийс приложением на электронном носителе / Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков,С.Б.Суворова; под ред.С.А.Теляковского.- 19-е изд.- М.: Просвещение, 2014

4.      МакарычевЮ.Н., Н.Г. Миндюк, Л.М. Короткова «Дидактические материалы по алгебре для 9класса М., Просвещение 2010

5.А.Н. Рурукин,С.А. Полякова «Поурочные разработки по алгебре 9 класс», М.: «ВАКО»,2011

6. ОГЭ (ГИА-9).Сборник заданий / Ю.А.Глазков , М.: Издательство Экзамен, 2015

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Календарно-тематическоепланирование 2017

 

№

 

Наименование разделов и тем

Тема урока

Кол.во часов

Дата по плану

Факт дата провед

примечание

1-2

 

Повторение

2

4.09

6.09

 

 

 

 

 Глава 1 Квадратичная функция.

22

 

 

 

 

 

Функции и их свойства

5

 

 

 

3

1

Функция. Область определения и область значений функции

1

9.09

 

 

3

2

Функция. Область определения и область значений функции

1

11.09

 

 

4

3

Свойства функции

1

13.09

 

 

5

4

Свойства функции

1

16.09

 

 

6

5

Свойства функции

1

18.09

 

 

7

 

Административная контрольная работа

1

20.09

 

 

 

 

Квадратный трехчлен

4

 

 

 

8

6

Квадратный трехчлен и его корни

1

23.09

 

 

9

7

Квадратный трехчлен и его корни

1

2509

 

 

10

8

Разложение квадратного трехчлена на множители.

1

27.09

 

 

11

9

Разложение квадратного трехчлена на множители.

1

30.09

 

 

12

10

Контрольная работа №1 «Свойства функции. Квадратный трехчлен».

1

2.10.

 

 

 

 

Квадратичная функция и ее график

8

 

 

 

13

11

 функции y=ax2 , ее график и свойства

1

4.10

 

 

14

12

функции y=ax2 ее график и свойства

1

7.10

 

 

15

13

Графики функций   и  .

1

9.10

 

 

16

14

Графики функций   и  .

1

14.10

 

 

17

15

Построение графика квадратичной функции.

1

16.10

 

 

18

16

Построение графика квадратичной функции.

1

18.10

 

 

19

17

Построение графика квадратичной функции.

1

21.10

 

 

20

18

Построение графика квадратичной функции.

1

23.10

 

 

 

 

Степенная функция . Корень n    -й степени

3

 

 

 

21

19

Функция у=хп.

1

25.10

 

 

22

20

Корень п—ой  степени.

1

28.10

 

 

23

21

Корень п—ой  степени.

1

6.11

 

 

24

22

Контрольная работа № 2 «Квадратичная функция. Степенная функция».

1

8.11

 

 

 

 

 Глава 2 Уравнения и неравенства с одной переменной

14

 

 

 

 

 

Уравнения  с одной переменной

8

 

 

 

25

1

Анализ контрольной работы. Целое уравнение и его корни

1

11.11

 

 

26

2

Целое уравнение и его корни

1

13.11

 

 

27

3

Целое уравнение и его корни.

1

15.11

 

 

28

4

Дробные рациональные уравнения

1

18.11

 

 

29

5

Дробные рациональные уравнения

1

20.11

 

 

30

6

Дробные рациональные уравнения.

1

22.11

 

 

31

7

Дробные рациональные уравнения

1

25.11

 

 

 

8

Дробные рациональные уравнения

1

27.11

 

 

 

 

 Неравенства с одной переменной

5

 

 

 

32

9

Решение неравенств второй степени с одной переменной

1

29.11

 

 

33

10

Решение неравенств второй степени с одной переменной

1

2.12

 

 

34

11

Решение неравенств методом интервалов

1

4.12

 

 

35

12

Решение неравенств методом интервалов.

1

6.12

 

 

36

13

Решение неравенств методом интервалов.

1

9.12

 

 

37

14

Контрольная работа № 3 «Уравнения и неравенства с одной переменной».

1

11.12

 

 

 

 

 Глава 3 Уравнения и неравенства с двумя переменными

17

 

 

 

 

 

Уравнения  с двумя переменными и их системы

10

 

 

 

38

1

Анализ контрольной работы. Уравнение с двумя переменными и его график

1

13.12

 

 

39

2

Уравнение с двумя переменными и его график

1

16.12

 

 

40

3

Графический способ решения систем уравнений

1

18.12

 

 

41

4

Графический способ решения систем уравнений

1

20.12

 

 

42

5

Решение систем уравнений второй степени

1

23.12

 

 

43

6

Решение систем уравнений второй степени

1

25.12

 

 

44

7

Решение систем уравнений второй степени

1

27.12

 

 

45

8

Решение задач с помощью систем уравнений второй степени

1

30.12

 

 

46

9

. Решение задач с помощью систем уравнений второй степени

1

15.01

 

 

47

10

Решение задач с помощью систем уравнений второй степени

1

17.01

 

 

 

 

Неравенства с двумя переменными и их системы

6

 

 

 

48

11

Неравенства с двумя переменными

1

20.01

 

 

40

12

Неравенства с двумя переменными

1

22.01

 

 

50

13

Системы неравенств с двумя переменными

1

24.01

 

 

51

14

Системы неравенств с двумя переменными

1

27.01

 

 

52

15

Системы неравенств с двумя переменными

1

29.01

 

 

53

16

Системы неравенств с двумя переменными

1

31.01

 

 

54

17

Контрольная работа № 4 «Уравнения и неравенства с двумя переменными».

1

3.02

 

 

 

Представленная информация была полезной?
ДА
60.92%
НЕТ
39.08%
Проголосовало: 1538

 

 Глава 4 Арифметическая и геометрическая прогрессии

15

 

 

 

 

 

Арифметическая прогрессия

7

 

 

 

55

1

Анализ контрольной работы. Последовательности

1

5.02

 

 

56

2

Последовательности

1

7.02

 

 

57

3

Определение   арифметической   прогрессии. Формула n-го члена арифметической про­грессии.

1

10.02

 

 

58

4

Определение   арифметической   прогрессии. Формула n-го члена арифметической про­грессии.

1

12.02

 

 

59

5

Формула суммы п первых членов арифмети­ческой прогрессии.

1

14.02

 

 

60

6

 Формула суммы п первых членов арифмети­ческой прогрессии.

1

17.02

 

 

61

7

Решение задач. Подготовка к контрольной работе

1

19.02

 

 

62

8

Контрольная работа №5  «Арифметическая прогрессия».

1

21.02

 

 

 

 

Геометрическая прогрессия

6

 

 

 

63

9

Анализ контрольной работы. Определение   геометрической   прогрессии. Формула n-го  1члена  геометрической  про­грессии

1

24.02

 

 

64

10

Определение   геометрической   прогрессии. Формула n-го  члена  геометрической  про­грессии

1

26.02

 

 

65

11

Формула n-го  члена  геометрической  про­грессии

1

28.02

 

 

66

12

Формула суммы п первых членов геометри­ческой прогрессии

1

3.03

 

 

67

13

Формула суммы п первых членов геометри­ческой прогрессии.

1

5.03

 

 

68

14

Формула суммы п первых членов геометри­ческой прогрессии.

1

7.03

 

 

69

15

Контрольная работа № 6  «Геометрическая прогрессия»

1

10.03

 

 

 

 

 Глава 5.Элементы комбинаторики и теории вероятностей

13

 

 

 

70

1

Анализ контрольной работы. Примеры комбинаторных задач

1

12.03

 

 

71

2

Примеры комбинаторных задач.

1

14.03

 

 

72

3

Перестановки

1

17.03

 

 

73

4

Перестановки

1

19.03

 

 

74

5

Размещения

1

21.03

 

 

75

6

Размещения

1

24.03

 

 

76

7

Сочетания

1

2.04

 

 

77

8

Сочетания

1

4.04

 

 

78

9

Перестановки. Размещения. Сочетания.

1

7.04

 

 

79

10

Относительная частота случайного события.

1

9.04

 

 

80

11

Вероятность равновозможных событий.

1

11.04

 

 

81

12

Обобщающий урок.

Сложение и умножение вероятностей. Подготовка к контрольной работе

1

14.04

 

 

82

13

 Контрольная работа №7 «Элементы комбинаторики и теории вероятностей»

1

16.04

 

 

 

 

Повторение

14

 

 

 

83

1

Анализ контрольной работы.  Функции и их свойства.

1

18.04

 

 

84

2

Функции и их свойства. Подготовка к ГИА

1

21.04

 

 

85

3

Функции и их свойства. Подготовка к ГИА

1

23.04

 

 

86

4

Квадратный трёхчлен. Подготовка к ГИА.

1

25.04

 

 

87

5

Квадратичная функция и её график. Подготовка к ГИА

1

28.04

 

 

88

6

Квадратичная функция и её график. Подготовка к ГИА

1

30.04

 

 

89

7

Степенная функция. Корень п—ой  степени.  Подготовка к ГИА

1

2.05

 

 

90

8

Степенная функция. Корень п—ой  степени.  Подготовка к ГИА.

1

5.05

 

 

91

9

Уравнения и неравенства с одной переменной. Подготовка ГИА

1

7.05

 

 

92

10

Уравнения и неравенства с одной переменной. Подготовка к ГИА

1

12.05

 

 

93

11

Уравнения и неравенства с двумя переменными. Подготовка к ГИА

1

14.05

 

 

94

12

Уравнения и неравенства с двумя переменными. Подготовка к ГИА.

1

16.05

 

 

 

95

96

 

13

Арифметическая и геометрическая прогрессии. Подготовка к ГИА

1

19.05

 

 

97

14

Итоговая контрольная работа

1

21.05

 

 

98

16

Анализ контрольной работы. .

1

23.05

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Рассмотрено ипринято           Согласовано                                     Утверждено

на заседанииМО                     Заместитель директора по УВР     Директор МОБУ СОШ №2

Протокол№_____                   ________Юмагужина З.А.              с. Инзер

от«___»_____20____ г.         «___» _____20____г.                       _________Идрисов Р.Н.

Руководитель МО                                                                            Приказ №____

 _______Шагисултанова А.М.                                                          от «____»_____20_____г.

 

 

 

 

 

 

 

 

 

Приложение

крабочей программе

 попредмету «Математика (алгебра) »

для 9 б класса

на2017-2018 учебный год

 

Срокреализации – 1 год

                                                                          

 

 

 

 

 

 

 

 

 

                                                                                             Составила

                                                                                        учитель  СунаргуловаГ.Б.                                                         

                                                                                                       

 

 

 

 

 

 

 

                                                        

 

 

 

 

 

 

 

 

                                                                    2017 год

 

 

 

 

1.Контрольно-измерительные материалы   Макарычев Ю.Н., Н.Г. Миндюк, Л.М.Короткова «Дидактические материалы по алгебре для 9 класса М., Просвещение 2010

 

 

II.Измерители, контроль знаний на 2017 — 2018 учебный год                             

Контрольнаяработа по теме:

«Функции и их свойства. Квадратный трехчлен»

 

Вариант 1

 

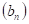111°. Дана функция . При каких значенияхаргумента ? Является ли эта функция возрастающей илиубывающей?

2°. Разложите на множители квадратный трехчлен:

     а) .

3°.Сократите дробь .

4.  Область определения функции g– отрезок . Найдите нули функции, промежуткивозрастания и убывания, область значений функции.

5.  Сумма положительных чисел а и bравна 50. При каких значениях а и b ихпроизведение будет наибольшим?

 

Вариант 2

 

1°. Дана функция . При каких значенияхаргумента ? Является ли эта функция возрастающей илиубывающей?

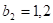112°. Разложите на множители квадратный трехчлен:

     а) .

3°.Сократите дробь .

4.  Область определения функции f– отрезок . Найдите нули функции, промежуткивозрастания и убывания, область значений функции.

5.  Сумма положительных чисел с и dравна 70. При каких значениях c и dих произведение будет наибольшим?

 

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верновыполнены 4 задания;

«3» — верновыполнены 3 задания.

 

 

 

 

Контрольнаяработа по теме:

«Квадратичная функция»

 

Вариант 1

 

1°. Постройте график функции .Найдите с помощью графика:

а) значение у при х = 0,5;

б) значения х, при которых  у = – 1;

в) нули функции; промежутки, в которых y> 0 и в которых y < 0;

г) промежуток, на котором функция возрастает.

2°. Найдите наименьшее значение функции  .

3.Найдите область значений функции , где .

4.  Невыполняя построения, определите, пересекаются ли парабола  и прямая . Еслиточки пересечения существуют, то найдите их координаты.

5.  Найдите значение выражения .

 

 

Вариант 2

 

1°. Постройте график функции .Найдите с помощью графика:

а) значение у при х = 1,5;

б) значения х, при которых  у = 2;

в) нули функции; промежутки, в которых y> 0 и в которых y < 0;

г) промежуток, на котором функция убывает.

2°. Найдите наибольшее значение функции  .

3.Найдите область значений функции , где .

4.  Невыполняя построения, определите, пересекаются ли парабола  и прямая . Еслиточки пересечения существуют, то найдите их координаты.

5.  Найдите значение выражения .

 

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верновыполнены 3, 4 задания;

«3» — верновыполнены 2 задания.

 

 

 

 

 

 

 

Контрольная работа по теме:

«Уравнения и неравенства с одной переменной»

 

Вариант 1

 

1°. Решите уравнение:

      а) .

2°. Решите неравенство:

      а) .

3°.Решите неравенство методом интервалов:

     а) .

4°.Решите биквадратное уравнение

.

5. При каких значениях т уравнение  имеетдва корня?

6. Найдите область определения функции

.

7. Найдите координаты точек пересечения графиков функций  и .

 

 

Вариант 2

 

1°. Решите уравнение:

      а) .

2°. Решите неравенство:

      а) .

3°.Решите неравенство методом интервалов:

     а) .

4°.Решите биквадратное уравнение

.

5. При каких значениях п уравнение  неимеет корней?

6. Найдите область определения функции

.

7. Найдите координаты точек пересечения графиков функций  и .

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верновыполнены 5, 6 заданий;

«3» — верновыполнены 4 задания.

 

 

 

Контрольная работа по теме:

«Уравнения и неравенства с двумя переменными»

 

Вариант 1

 

1°. Решите систему уравнений

2°. Периметр прямоугольника равен 28 м, а его площадь   равна   40 м2. Найдите  стороны прямоугольника.

3°.Изобразите на координатной плоскости множество решений системы неравенств

4. Не выполняя построения, найдите координаты точек пересеченияпараболы  и прямой .

5. Решите систему уравнений

 

 

Вариант 2

 

1°. Решите систему уравнений

2°. Одна из сторон прямоугольника на 2 см больше другой стороны.Найдите стороны прямоугольника, если его площадь равна   120см2. 

3°.Изобразите на координатной плоскости множество решений системы неравенств

4. Не выполняя построения, найдите координаты точек пересеченияокружности  и прямой .

5. Решите систему уравнений

 

 

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верновыполнены 4 задания;

«3» — верновыполнены 3 задания.

 

 

 

 

 

 

 

 

 

 

 

 

Контрольная работа по теме:

«Арифметическая прогрессия»

 

Вариант 1

 

1°. Найдите  двадцать  третий  член арифметической прогрессии , если  и  .

2°. Найдите сумму шестнадцати первых членов арифметическойпрогрессии: 8; 4; 0; … . 

3.  Найдите сумму шестидесяти первых членов последовательности , заданной формулой .

4. Является ли число 54,5 членом арифметической прогрессии , в которой  и ?

5.  Найдите  сумму  всех  натуральных  чисел, кратных 3 и непревосходящих 100.

 

 

Вариант 2

 

1°. Найдите  восемнадцатый  член арифметической прогрессии , если  и  .

2°. Найдите сумму двадцати первых членов арифметической прогрессии:– 21; – 18; – 15; … .

3.  Найдите сумму сорока  первых  членов последовательности , заданной формулой .

4. Является ли число 30,4 членом арифметической прогрессии , в которой  и ?

5.  Найдите  сумму  всех  натуральных  чисел, кратных 7 и непревосходящих 150.

 

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верновыполнены 3, 4 задания;

«3» — верновыполнены 2 задания.

 

 

 

 

Контрольнаяработа по теме:

 «Геометрическая прогрессия»

 

Вариант 1

1°. Найдите  седьмой  член геометрической прогрессии , если  и  .

2°. Первый член геометрической прогрессии  равен2, а знаменатель равен 3. Найдите сумму шести первых членов этой прогрессии.

3.  Найдите сумму бесконечной геометрической прогрессии: 24; –12;6; … .

4. Найдите сумму девяти  первых  членов геометрической прогрессии  с положительными членами, зная, что  и .

5.  Представьте  в  виде  обыкновенной  дроби бесконечнуюдесятичную дробь: 

       а) 0,(27);         б) 0,5(6).

 

 

Вариант 2

1°. Найдите  шестой  член геометрической прогрессии , если  и  .

2°. Первый член геометрической прогрессии  равен6, а знаменатель равен 2. Найдите сумму семи первых членов этой прогрессии.

3.  Найдите сумму бесконечной геометрической прогрессии: – 40; 20;– 10; … .

4. Найдите сумму восьми  первых  членов геометрической прогрессии  с положительными членами, зная, что  и .

5.  Представьте  в  виде  обыкновенной  дроби бесконечнуюдесятичную дробь: 

       а) 0,(153);         б) 0,3(2).

 

 

 

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верновыполнены 3, 4 задания;

«3» — верновыполнены 2 задания.

 

 

 

Контрольнаяработа по теме:

«Элементы комбинаторики и теории вероятностей»

 

Вариант 1

 

1°. Сколькими способами могут разместиться 5 человек в салонеавтобуса на 5 свободных местах?

2°. Сколько трехзначных чисел, в которых нет одинаковых цифр, можносоставить из цифр 1, 2, 5, 7, 9?

3°. Победителю  конкурса  книголюбов разрешается выбрать две книгииз 10 различных книг. Сколькими способами он может осуществить этот выбор?

4°. В доме 90 квартир, которые распределяются по жребию. Каковавероятность того, что жильцу не достанется квартира на первом этаже, если такихквартир 6?

5.  Из 8 мальчиков и 5 девочек надо выделить для работы напришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можносделать?

6.  На четырех карточках  записаны  цифры  1, 3, 5, 7.  Карточкиперевернули и перемешали. Затем наугад последовательно положили эти карточки вряд одну за другой и открыли. Какова вероятность того, что в результатеполучится число 3157?

 

Вариант 2

 

1°. Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 5,7, 9 без повторений цифр?

2°. Из 8 учащихся класса, успешно выступивших на школьной олимпиаде,надо выбрать двух для участия в городской олимпиаде. Сколькими способами можносделать этот выбор?

3°. Из 15 туристов надо выбрать дежурного и его помощника. Какимиспособами это можно сделать?

4°. Из 30 книг, стоящих на полке, 5 учебников, а остальныехудожественные произведения. Наугад берут с полки одну книгу. Каковавероятность того, что она не окажется учебником?

5.  Из 9 книг и 6 журналов надо выбрать 2 книги и 3 журнала.Сколькими способами можно сделать этот выбор?

6.  На пяти карточках  написаны  буквы  а, в, и, л, с.  Карточкиперевернули и перемешали. Затем наугад последовательно положили эти карточки вряд одну за другой и открыли. Какова вероятность того, что в результатеполучится слово «слива»?

 

 

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верновыполнены 5 заданий;

«3» — верновыполнены 4 задания.

 

Итоговаяконтрольная работа по алгебре

Вариант 1

1°. Упростите выражение .

2°. Решите систему уравнений

3°. Решите неравенство .

4°. Представьте выражение  в виде степени соснованием а.

5.  Постройте  график  функции  .Укажите, при каких значениях х функция принимает положительные значения.

6.  В фермерском хозяйстве под гречиху было отведено два участка.С первого участка собрали 105 ц гречихи, а со второго, площадь которого на 3 габольше, собрали 152 ц. Найдите площадь каждого участка, если известно, чтоурожайность гречихи на первом участке была на 2 ц с 1 га больше, чем на втором.

 

Вариант 2

 

1°. Упростите выражение .

2°. Решите систему уравнений

3°. Решите неравенство .

4°. Представьте выражение  в виде степени соснованием у.

5.  Постройте  график  функции  .Укажите, при каких значениях х функция принимает отрицательные значения.

6.  Из пункта А в пункт В,  расстояние  между которыми   45 км, выехал  велосипедист.  Через 30 мин вслед за ним выехал второй велосипедист,который прибыл в пункт В на 15 мин раньше первого. Какова скорость первоговелосипедиста, если она на 3 км/ч меньше скорости второго?

 

 

 

Критерииоценки:

«5» — верновыполнены все задания;

«4» — верно выполнены5 заданий;

«3» — верновыполнены 4 задания.

 

 

 

III.Контроль над выполнением практической части программы

№

Практическая часть

I четверть

II четверть

III

четверть

IV

четверть

Итого за год

1

Контрольные работы

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Геометрия

 

Контрольная работа по теме:

«Векторы. Метод координат»

 

Вариант 1


Поделиться статьей
Автор статьи
Анастасия
Анастасия
Задать вопрос
Эксперт
Представленная информация была полезной?
ДА
60.92%
НЕТ
39.08%
Проголосовало: 1538

или напишите нам прямо сейчас:

Написать в WhatsApp Написать в Telegram

Электроэнергетические системы и сети

Поделиться статьей

Поделиться статьейПоделиться статьей Автор статьи Анастасия Задать вопрос Эксперт Представленная информация была полезной? ДА 60.92% НЕТ 39.08% Проголосовало: 1538


Поделиться статьей

Электроснабжение производственных объектов

Поделиться статьей

Поделиться статьейПоделиться статьей Автор статьи Анастасия Задать вопрос Эксперт Представленная информация была полезной? ДА 60.92% НЕТ 39.08% Проголосовало: 1538


Поделиться статьей

Электроснабжение

Поделиться статьей

Поделиться статьейПоделиться статьей Автор статьи Анастасия Задать вопрос Эксперт Представленная информация была полезной? ДА 60.92% НЕТ 39.08% Проголосовало: 1538


Поделиться статьей

Электрооборудование и электрохозяйство предприятий организаций и учреждений

Поделиться статьей

Поделиться статьейПоделиться статьей Автор статьи Анастасия Задать вопрос Эксперт Представленная информация была полезной? ДА 60.92% НЕТ 39.08% Проголосовало: 1538


Поделиться статьей

или напишите нам прямо сейчас:

Написать в WhatsApp Написать в Telegram

X-PDF

Заявка
на расчет
×

или напишите нам прямо сейчас:

Написать в WhatsApp Написать в Telegram